Корреляция (значения).
Запрос «Коэффициент корреляции Пирсона» .
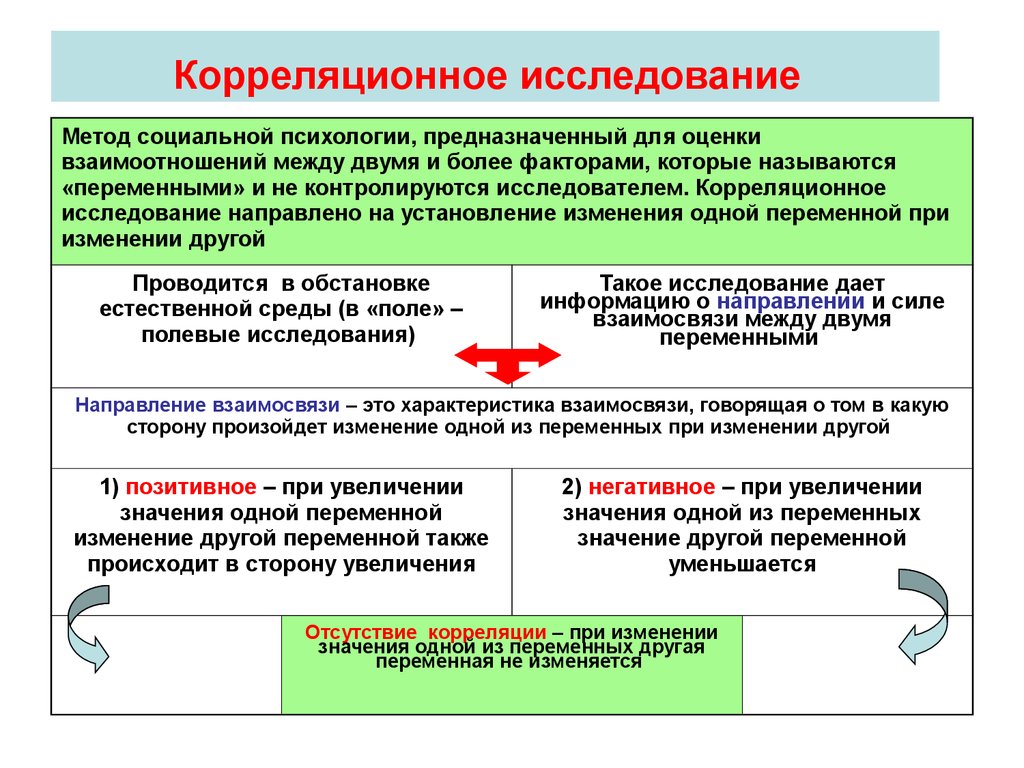
Корреля́ция (от лат. correlatio «соотношение, взаимосвязь»), или корреляционная зависимость — статистическая взаимосвязь двух или более случайных величин (либо величин, которые можно с некоторой допустимой степенью точности считать таковыми). При этом изменения значений одной или нескольких из этих величин сопутствуют систематическому изменению значений другой или других величин.
Математической мерой корреляции двух случайных величин служит корреляционное отношение
η
{\displaystyle \mathbf {\eta } }
либо коэффициент корреляции
R
{\displaystyle \mathbf {R} }
(или
r
{\displaystyle \mathbf {r} }
). В случае если изменение одной случайной величины не ведёт к закономерному изменению другой случайной величины, но приводит к изменению другой статистической характеристики данной случайной величины, то подобная связь не считается корреляционной, хотя и является статистической.
Впервые в научный оборот термин корреляция ввёл французский палеонтолог Жорж Кювье в XVIII веке. Он разработал «закон корреляции» частей и органов живых существ, с помощью которого можно восстановить облик ископаемого животного, имея в распоряжении лишь часть его останков. В статистике слово «корреляция» первым стал использовать английский биолог и статистик Фрэнсис Гальтон в конце XIX века.
Содержание 1 Корреляция и взаимосвязь величин
2 Показатели корреляции 2.1 Параметрические показатели корреляции 2.1.1 Ковариация
2.1.2 Линейный коэффициент корреляции 2.2 Непараметрические показатели корреляции 2.2.1 Коэффициент ранговой корреляции Кендалла
2.2.2 Коэффициент ранговой корреляции Спирмена
2.2.3 Коэффициент корреляции знаков Фехнера
2.2.4 Множественный коэффициент корреляции
2.2.5 Коэффициент множественной ранговой корреляции (конкордации) 2.3 Свойства коэффициента корреляции 3 Корреляционный анализ 3.1 Ограничения корреляционного анализа
3.2 Область применения 4 См. также
5 Примечания
6 Литература
7 Ссылки
Методы изучения корреляционных связей